~ Mengajar dengan Metode Kecerdasan Majemuk ~

+ PERKEMBANGAN INDIVIDU (ANAK) +

APLIKASI PEMODELAN MATEMATIKA SEDERHANA DI BIDANG PERTANIAN

APLIKASI PEMODELAN MATEMATIKA SEDERHANA DI BIDANG PERTANIAN

(Penjadwalan Irigasi Berselang)

1.    Pengantar

Salah satu aplikasi dari pemodelan matematika sederhana pada bidang pertanian adalah pada penjadwalan sistem pengairan sawah (irigasi) secara berselang (bergantian). Untuk memperoleh hasil yang maksimal dari hasil pertanian, tentu harus juga memperhatikan kesesuaian antara jenis tanaman dengan ketersediaan air pada lahan tersebut. Dan salah satu usaha yang dapat dilakukan untuk memenuhi pengairan pada lahan persawahan adalah dengan cara irigasi.

Irigasi merupakan cara pemberian air secara buatan untuk menambah kekurangan air yang dibutuhkan oleh tanaman. Irigasi pada tanaman diberikan dengan cara penggenangan. Hal ini dilakukan agar pemberian air yang cukup dan tetap stabil ke area persawahan guna menjamin produksi dari tanaman tersebut. Air irigasi ini biasanya diberikan dengan cara berselang dimana penggenangannya dilakukan dengan ukuran (volume) tertentu dan pengairan berikutnya dilakukan pada waktu (periode) tertentu setelah genangan air surut.

Sebagian besar, para petani dalam skala yang lebih besar, seringkali menerapkan sistem pengairan secara kurang efisien. Sebagian besar petani kita menerapkan irigasi dengan satu prinsip mengairi lahannya dengan jumlah air (volume air) sebanyak mungkin tanpa memperhatikan kebutuhan air untuk jenis tanaman yang berbeda-beda, atau tanpa menghiraukan kebutuhan optimum tanaman. Penerapan irigasi yang tidak efisien juga terjadi melalui cara pemberian air yang tidak tepat baik jumlah dan waktunya. Oleh karenanya, petani harus mengetahui secara pasti kebutuhan air optimum untuk setiap tanaman dan lama waktunya untuk melakukan sekali pengairan hingga kebutuhan air tanaman tercukupi.

Efisiensi irigasi dapat ditingkatkan dengan membuatkan jadwal irigasi itu sendiri. Penjadwalan ini berartii melakukan perencanaan waktu dan jumlah pemberian air irigasi sesuai dengan kebutuhan air tanaman. Suplai air yang terbatas dapat menurunkan produksi tanaman sedangkan, suplai air yang berlebihan selain dapat menurunkan produksi tanaman juga dapat mengurangi efisiensi penggunaan air.

Pada masalah penjadwalan irigasi tersebut, dapat digunakan pemodelan matematika. pemodelan matematika adalah model yang menggunakan konsep-konsep matematika seperti konstanta, variabel, fungsi, persamaan dan sebagainya yang disusun untuk tujuan tertentu (Meyer & Olnick, 1978). Misalkan kita akan melakukan pengairan sawah untuk tanaman padi

2.    Langkah-Langkah Pemodelan Matematika

Langkah-langkah dalam pemodelan matematika mengidentifikasikan faktor-faktor yang dominan berpengaruh, setelah itu kemudian memberikan asumsi-asumsi yang akan diambil. Faktor-faktor yang berpengaruh dengan perimbangan air dalam sistem hidrologi sawah yang mempengaruhi volume genangan air sawah. Secara umum, perimbangan air dalam sistem hidrologi berkaitan dengan komponen air yang masuk dan keluar. Komponen air yang hilang meliputi perkolasi (penyaringan), evatranspirasi, drainase (penyaluran air) permukaan, dan rembesan. Sedangkan, komponen air yang masuk meliputi curah hujan dan irigasi. Komponen air yang masuk menyebabkan bertambahnya volume air genangan, sedangkan komponen air yang keluar menyebabkan berkurangnya volume air genangan. Adapun beberapa asumsi yang dapat diduga, yakni:

• Tanah sawah sudah dijenuhkan terlebih dahulu sebelum diakukan penggenangan. Hal ini berarti bahwa volume air yang diperhitungkan hanya volume air yang terdapat pada permukaan. Dengan asumsi lain, bahwa volume genangan air merupakan hasil kali luas lahan dengan tinggi genangan.
• Tinggi genangan air awal sebesar 50 mm dan pengaliran selanjutnya dilakukan ketika genangan air sebesar 10 mm (Sulisilawati-Studi kasus daerah irigasi Tinalun: 2002)
• Lamanya waktu penggenangan tidak diperhitungkan
• Kehilangan air hanya terjadi melalui proses perkolasi dan evatranspirasi
• Penambangan volume air terjadi karena adanya curah hujan efektif
• Tidak terjadi kehilangan air karena drainase permukaan dan rembesan

Misalkan hal-hal tersebut di atas dapat disimbolkan sebagai berikut:

V        :      volume genangan air pada permukaan sawah (mm³)

h        :      tinggi genangan air (mm)

p        :      panjang lahan (mm)

l         :      lebar lahan (mm)

La      :      luas lahan (mm²)

P        :      laju perkolasi (mm/hari)

ET      :      evatranspirasi (mm/hari)

Ch      :      laju curah hujan efektif (mm³/hari)

t         :      waktu yang dibutuhkan dalam satu periode penggenangan (hari)

berdasarkan pemisalan variabel dan asumsi di atas, maka model matematikanya dapat dirumuskan sebagai berikut:

Lahan tersebut diasumsikan berbentuk persegi dengan panjang p dan lebar l. Dengan demikian, luas lahan tersebut dapat dirumuskan sebagai berikut:

La = p x l

Misalkan, pada setiap saat t ketinggian genangan air adalah     h = h (t)

maka rumus volume ketinggian air setiap saat pada ketinggian h dirumuskan sebagai berikut:

V(t) = La(t) x h(t)     ..................................... (1)

Akan ditentukan (dh/dt) saat ketinggian air h. Dengan turunan implisit terhadap t dari kedua ruas persamaan (1) memberikan :

Ketinggian genangan air akan berkurang karena adanya kehilangan air akibat adanya perkolasi dan evatranspirasi. Sedangkan, ketinggian air akan bertambah karena adanya penambahan volume air akibat curah hujan efektif. Dengan demikian ( dV / dt ) dapat dirumuskan sebagai berikut:

Laju perubahan volume air harian karena Evatranspirasi dan Perkolasi sama dengan Luas Lahan dikali dengan Laju Evatranspirasi dan Perkolasi dimana:

P        :      laju perkolasi (mm/hari)

ET      :      evatranspirasi (mm/hari)

Ch      :      laju curah hujan efektif (mm³/hari)

Dengan demikian laju perubahan ketinggian air dirumuskan sebagai berikut:

Agar diperoleh suatu fungsi h terhadap waktu maka dilakukan integral terhadap t pada kedua ruas dari persamaan (2)

pada saat t = 0, maka h awal dimisalkan sebagai h₀ maka diperoleh:

Sehingga didapat: C = - h₀

Karena nilai C = -h₀ maka:

jadi, rumus untuk menentukan waktu (t ) yang diperlukan ketika genangan air berkurang hingga h adalah

Dari rumus di atas, diperoleh suatu rumus untuk menentukan lamanya waktu penggenangan dalam hari, yakni t (hari). Setelah penggenangan dilakukan selama periode t (hari) maka penggenangan selanjutnya dapat dilakukan.

Teladan:

Suatu lahan pertanian di wilayah Suela-Pringgabaya ditanami Padi. Lahan tersebut berbentuk persegi panjang dengan luas lahan 200 m². Jenis tanah yang dipakai pada lahan tersebut yaitu tanah berlempung dengan laju perkolasi 2 mm/hari dan laju evatranspirasinya adalah 5 mm/hari. Rata-rata curah hujan pada daerah tersebut adalah 137.113 mm³/hari. Ketinggian genangan air mula-mula sesaat setelah dilakukan pengaliran adalah 5 cm. Berapakah lama waktu yang dibutuhkan untuk melakukan satu periode penggengan sehingga air genangan surut sampai dengan 1 cm?

Penyelesaian:

h₀      =   50 mm

h       =   10 mm

La     =   200 m² = 2 x 10⁸ mm²

ET     =   5 mm/hari

P       =   2 mm/hari

Ch     =   137.113 mm³/hari

Waktu yang diperlukan untuk melakukan sekali penggenangan adalah 

Jadi, waktu yang dibutuhkan untuk melakukan satu kali penggenangan adalah 6 hari. Sehingga, 5 hari setelah dilakukan pengaliran, petani harus kembali melakukan pengaliran air ke lahan sawah.

3.    kesimpulan

Dengan pemodelan matematika ini dapat disimpulkan beberapa pernyataan, yakni:

1.     Besarnya perubahan ketinggian air dapat diketahui dengan mempertimbangkan laju perkolasi, evatranspirasi, dan curah hujan

2.     Lamanya waktu penggenangan bergantung pada besarnya laju perkolasi, evatranspirasi dan curah hujan

3.     Dengan diketahui periode penggenangan (t ) maka pengaliran air selanjutnya dapat dilakukan setelah penggenangan dilakukan selama (t ).

Psikologi Pendidikan-Sebuah tinjauan Studi Psikologis

PSIKOLOGI PENDIDIKAN

Sebuah tinjauan Studi Psikologis

https://youtu.be/1wN99i0kaRE

Jika memperhatikan vidio tersebut, dapatkah kita kemudian menemukan Sifat-Sifat Umum Aktivitas Manusia?

PENYELESAIAN MODEL MATEMATIKA

Pada pembahasan pertama telah dibahas mengenai pemodelan matematika terkait dengan tahap-tahap pembentukan model matematika tersebut. Model matematika yang diperoleh dari suatu masalah matematika yang diberikan, selanjutnya dipecahkan dengan aturan-aturan yang ada untuk memperoleh nilai variabelnya. Kemudian jika nilai variabel telah diperoleh, perlu diuji hasil itu atau dilakukan interpretasi untuk mengetahui apakah nilai itu valid atau tidak valid. Hasil yang valid akan menjawab secara tepat model matematikanya. Hasil seperti inilah yang disebut solusi matematika. Jika nilai variabelnya tidak valid atau tidak memenuhi model matematika maka solusi masalah belum ditemukan, dan perlu dilakukan pemecahan ulang atas model matematikanya. Secara umum proses pemodelan dan pemecahan model dapat dilihat seperti pada Bagan di bawah ini.

Abstraksi      : gambar atau hal yang mewakili suatu obyek nyata, sesuatu tanpa memperhatikan jenis obyek sebenarnya. Misalnya, dalam sebuah soal cerita digunakan simbol x, y untuk mewakili suatu obyek. Dalam hal ini symbol x atau y merupakan abstraksi dari obyek yang dibicarakan.

Idealisasi     : sesuatu hal dipandang lengkap, utuh, sempurna walaupun dalam model itu tidak seperti sesungguhnya Misalnya, seorang siswa menggambar bangun segita, akan tetapi pada bagian salah satu sisi tidak tepat lurus seperti yang lainnya. Namun dalam pemahaman kita, gambar itu sudah lengkap(ideal).

interpretasi  : tafsiran secara teoritis terhadap sesuatu

Agar lebih memantapkan pemahaman pada pembahasan ini, berikut akan diberikan beberapa contoh masalah-masalah matematika beserta penyelesaiannya pada beberapa bidang, seperti di bidang aritmetika, aljabar, geometri dan pengukuran, trigonometri dan peluang.

1.    Aritmetika

Contoh 1:

Diketahui volume sebuah kubus yaitu 27 cm³, tentukan panjang rusuk kubus tersebut.

Penyelesaian :

Rumus volume suatu kubus adalah sisi kali sisi kali sisi atau disingkat dengan s³ yang diketahui sama dengan 27 cm³ atau s³ = 27 sehingga panjang sisi atau rusuk dari kubus tersebut adalah sama dengan 3 cm.

Contoh 2:

Pertambahan penduduk di kota Selong, tiap tahun mengikuti aturan barisan geometri. Tahun 2005 pertambahannya sebanyak 6 orang dan pada tahun 2007 sebanyak 54 orang. Tentukan pertambahan penduduk pada tahun 2010. 

Penyelesaian :

Misalkan pertambahan penduduk pada tahun 2005 adalah  u₁ = 6 dan pertambahan penduduk pada tahun 2007 adalah  u₃ = 54. Pertambahan penduduk di kota Selong mengikuti aturan barisan geometri maka diperoleh :

u₃        =   54

u₁r^3-1    =   54

6r²       =   54

r²         =   9

r = -3 atau r = 3

Untuk nilai r = -3 tidak mungkin merupakan penyelesaian masalah karena akan mendapatkan hasil negatif. Jadi yang digunakan adalah nilai  r = 3. Menentukan pertambahan penduduk pada tahun 2010 berarti menentukan u₆ yaitu sama dengan u₆ = u₁r^6-1 = 6 x 3⁵ = 1458.

Jadi pertambahan penduduk kota Selong pada tahun 2010 adalah sebanyak 1458 orang.

2.    Aljabar

Berikut ini akan dibahas masalah-masalah matematika, pemodelan dan penyelesaian model matematikanya untuk bidang aljabar. Tidak semua masalah matematika dalam bidang aljabar dibahas, hanya untuk masalah-masalah yang menyangkut persamaan, pertidaksamaan baik linear maupun kuadrat serta sistem persamaan linear dengan dua varibel saja. Masalah-masalah tersebut dipilih karena kita telah mempelajari konsep mengenai persamaan, pertidaksamaan baik linear maupun kuadrat serta sistem persamaan linear dengan dua varibel. Jadi model matematika dalam bidang ini merupakan penyelesaian persamaan, pertidaksamaan atau sistem linear dengan dua variabel. Penyelesaian persamaan, pertidaksamaan atau sistem persamaan adalah suatu konstanta atau nilai yang memenuhi persamaan, pertidaksamaan atau sistem persamaan tersebut.

Contoh 1:

Nadia mengendarai sepeda motor dengan kecepatan 40 km/jam. Dari tempat yang sama, sejam kemudian Sinta mengenderai sepeda motor ke arah yang sama dengan kecepatan 56 km/jam. Tentukan setelah berapa jam perjalanan Sinta menyalip atau mendahului Nadia.

Penyelesaian:

Diketahui     : kecepatan sepeda motor Nadia sama dengan 40 km/jam dan Sinta 56 km/jam.

Ditanyakan : setelah berapa jam Sinta mendahului Nadia?

Misalkan lama perjalanan Sinta sampai mendahului Nadia adalah t jam. Nadia berangkat 1 jam lebih dulu dari Sinta maka ketika didahului Sinta, ia telah berjalan selama  t + 1 jam. Kecepatan motor Nadia 40 km/jam, maka jarak yang ditempuh Nadia sampai didahului Sinta adalah           40(t + 1) km. Selanjutnya kecepatan motor Sinta adalah 56 km/jam maka selama t jam, Sinta menempuh jarak 56t. Pada saat Sinta mendahului Nadia berarti jarak yang ditempuh adalah sama sehingga diperoleh model matematika yang merupakan persamaan linear dengan satu variabel yaitu 40(t + 1) = 56t. Penyelesaian persamaan linear  40(t + 1) = 56t adalah sebagai berikut.

40(t + 1) = 56t

40t + 40 = 56t

56t + 40t = 40

16t  = 40

t = 2,5 

Jadi Sinta mendahului Nadia setelah ia berjalan selama 2,5 jam.

   

Contoh 2:

Irwansyah mempunyai selembar seng dengan panjang 80 cm dan lebar 60 cm. Ia ingin mengecilkan seng tersebut dengan memotong panjang dan lebarnya sama besar sehingga luas seng yang diperoleh menjadi setengah luas mula-mula. Berapa panjang dan lebar seng yang harus dipotong?

Penyelesaian :

Diketahui : Selembar seng berbentuk persegi panjang dengan panjang 80 cm dan lebar 60 cm. Dari yang diketahui ini diperoleh luas seng yaitu seluas 80 x 60 = 4800 cm².

Ditanyakan : Berapa panjang dan lebar seng yang harus dipotong sehingga luas seng yang diperoleh menjadi setengah luas mula-mula.

Misalkan seng dipotong panjang dan lebarnya sepanjang x cm sehingga diperoleh panjang dan lebar seng masing-masing adalah  80 − x cm dan  60 − x cm. Luas seng setelah dipotong adalah setengah dari luas mula-mula sehingga diperoleh

½ x 4800 = 24000

Jadi diperoleh model matematika dari masalah di atas yaitu

(80 − x ) dan (60 – x) = 2400

Persamaan di atas merupakan persamaan kuadrat. Selanjutnya dilakukan penyelesaian modelnya dengan cara sebagai berikut.

(80 − x ) dan (60 – x) = 2400

4800 – 80x – 60x + x² = 0

4800 – 140x + x² = 0

(x – 120) (x – 20) = 0

x – 120 = 0 atau x – 20 = 0

x = 120 atau x = 20

Jadi diperoleh nilai x = 120 atau x  = 20 yang memenuhi persamaan kuadrat 

(80 − x ) dan (60 – x) = 2400.

Nilai  x = 120 tidak mungkin merupakan penyelesaian masalah karena panjang seng adalah 80 cm. Jadi panjang dan lebar seng dipotong sepanjang 20 cm agar luas seng yang diperoleh sama dengan setengah luas mula-mula.

Contoh 3: Dalam suatu pertandingan, harga karcis pada kelas utama dijual Rp 25.000.- per orang, sedangkan kelas ekonomi Rp.10.000,- per orang. Jika banyak karcis yang terjual 860 lembar, dengan pemasukan Rp. 13.400.000,-, tentukanlah jumlah penonton kelas utama.

Penyelesaian :

Diketahui    :  harga karcis kelas utama Rp. 25.000,-, kelas ekonomi Rp.10.000, dan karcis terjual 860 lembar, dengan pemasukan Rp. 13.400.000,-

Ditanyakan  : Jumlah penonton kelas utama.

Misalkan jumlah penonton kelas utama adalah x, dan kelas ekonomi y. Banyak karcis yang terjual 860 lembar sehingga diperoleh persamaan  x + y =860 yang memberikan pemasukan sebesar Rp. 13.400.000,-. Untuk mempermudah memahami masalahnya, dibuatkan terlebih dahulu tabel bantuannya sebagai berikut

Kelas	Jumlah Tiket	Harga (Rp)
Utama	x	25.000,-
Ekonomi	y	10.000,-
Jumlah	860	13.400.000,-

Dengan memperhatikan tabel di atas, maka diperoleh model matematika dari masalah tersebut, dimana modelnya merupakan sistem persamaan linier dengan dua variabel, yaitu

Tahapan berikutnya adalah menyelesaikan model (persamaan) tersebut di atas, yaitu misalnya dengan menggunakan salah satu model yang ada

x + y = 860 25x + 10y = 13400	x 10 x 1	10x + 10y = 8600 25x + 10y = 13400
		15x           = 4800 x               = 420

Lakukan substitusi ke salah satu persamaan awal dengan berdasar pada variabel yang sudah diketahui. Misalnya x + y = 860, maka akan diperoleh:

x + y = 860 420 + y = 860 y = 440

Jadi, banyak penonton kelas utama sebanyak 420 orang dan kelas ekonomi sebanyak 440 orang.

3.    Geometri dan Pengukuran

Contoh  : Diberikan sebuah kotak dengan ukuran panjang, lebar dan tinggi masing, masing sama dengan 60, 54 dan 42 cm. Diberikan pula beberapa kubus kecil dengan panjang rusuk sama dengan 6 cm. Tentukan berapa banyak kubus yang dapat dimasukkan dalam kotak. 

Penyelesaian :

Diketahui  : panjang, lebar dan tinggi suatu kotak yaitu 60, 54 dan 42 cm sehingga diperoleh volume kotak itu sebesar 60 x 54 x 42 = 136.080 cm³

                    panjang rusuk sebuah kubus 6 cm sehingga volume kubus tersebut adalah 

                    6 x 6 x 6 = 216 cm³

Ditanyakan  : banyak kubus yang dapat dimasukkan dalam kotak.

Misalnya banyak kubus tersebut adalah n maka

n =	Volume kotak	=	136.080	= 630
	Volume kubus		216

Jadi banyak kubus yang dapat dimasukkan ke dalam kotak tersebut adalah 630 kubus

4.    Trigonometri

Pada bagian ini, masalah-masalah matematika yang akan dibahas model dan penyelesaiannya adalah yang terkait dengan dalil pythagoras dan perbandingan trigonometri.

Contoh:

Sebuah tempat air minum berbentuk tabung dengan tinggi tabung 15 cm dan jari-jari alasnya 4 cm. Pada tabung tersebut diletakkan sedotan dengan posisi seperti pada gambar berikut

tentukan panjang sedotan tersebut

Penyelesaian:

Diketahui: Tinggi dan jari-jari alas sebuah tabung tempat air minum adalah 15 cm dan 4 cm, sehingga diameter tabung adalah 8 cm.

Ditanyakan :  panjang sedotan yang diletakkan pada tabung

Misalkan panjang sedotan tersebut adalah x, maka dengan menggunakan dalil Pythagoras, kita dapat menentukan nilai x yaitu sebagai berikut:

x² = 8² + 152  = 64 + 225  = 289

x² = 17

jadi panjang sedotan yang ada dalam tabung tersebut adalah 17 cm.

5.    Peluang

Masalah matematika yang terkait dengan peluang akan kita kaji hanya khusus yang terkait dengan masalah permutasi dan kombinasi serta konsep peluang sederhana berikut ini.

Contoh 1 :

Dalam sebuah ruangan pertunjukkan teater, masih tertinggal 5 kursi kosong, tetapi masih ada 9 orang yang akan memasuki ruangan pertunjukan tersebut. Tentukan ada berapa cara kursi kosong tersebut dapat diduduki oleh kesembilan orang tersebut.

Penyelesaian :

Masalah di atas tidak mempertimbangkan urutan orang yang akan menduduki kelima kursi di ruang pertunjukan, maka masalah tersebut merupakan masalah kombinasi.

Dari sini diperoleh

9C5	=	9!	=	9.8.7.6.5.4.3.2.1
		(9 – 5)! . 5!		4.3.2.1.5.4.3.2.1
			=	9 . 8 . 7 . 6	=	126
				4 . 3 . 2 . 1

Jadi banyak cara 5 kursi kosong di ruangan pertunjukan dapat diduduki oleh kesembilan orang tersebut adalah sebanyak 126 cara.

Contoh2 :

Suatu kelas terdiri atas 28 siswa putra dan 12 siswa putri. Kelas tersebut akan memilih seorang ketua kelas dimana baik siswa putra maupun putri mempunyai hak yang sama untuk dipilih. Tentukan berapa peluang terpilih ketua kelas seorang siswa putri.

Penyelesaian :

Diketahui banyaknya siswa putri sebanyak 12 orang dan jumlah seluruh siswa dalam kelas tersebut ada sebanyak 30 orang, maka peluang terpilih ketua kelas seorang siswa putri adalah sebesar

12	atau	2
30		5

Pemodelan Matematika_1

PEMODELAN MATEMATIKA (MATHEMATICAL MODELING)

Model adalah representasi penyederhanaan dari sebuah realita yang complex (biasanya bertujuan untuk memahami realita tersebut) dan mempunyai feature yang sama dengan tiruannya dalam melakukan task atau menyelesaikan permasalahan. Model adalah karakteristik umum yang mewakili sekelompok bentuk yang ada, atau representasi suatu masalah dalam bentuk yang lebih sederhana dan mudah dikerjakan. Dalam matematika, teori model adalah ilmu yang menyajikan konsep-konsep matematis melalui konsep himpunan, atau ilmu tentang model-model yang mendukung suatu sistem matematis. Teori model diawali dengan asumsi keberadaan obyek-obyek matematika (misalnya keberadaan semua bilangan) dan kemudian mencari dan menganalisis keberadaan operasi-operasi, relasi-relasi, atau aksioma-aksioma yang melekat pada masingmasing obyek atau pada obyek-obyek tersebut. Indenpensi dua hukum matematis yang lebih dikenal dengan nama axiom of choice, dan contnuum hypothesis dari aksioma-aksioma teori himpunan (dibuktikan oleh Paul Cohen dan Kurt Godel) adalah dua hasil terkenal yang diperoleh dari teori model. Telah dibuktikan bahwa axiom of choice dan negasinya konsisten  dengan aksioma-aksioma Zermelo Fraenkel dalam teori himpunan dan hasil yang sama juga dipenuhi oleh continuum hypothesis. Model matematika yang diperoleh dari suatu masalah matematika yang diberikan, selanjutnya diselesaikan dengan aturan-aturan yang ada. Penyelesaian yang diperoleh, perlu diuji untuk mengetahui apakah penyelesaian tersebut valid atau tidak. Hasil yang valid akan menjawab secara tepat model matematikanya dan disebut solusi matematika. Jika penyelesaian tidak valid atau tidak memenuhi model matematika maka solusi masalah belum ditemukan, dan perlu dilakukan pemecahan ulang atas model matematikanya.

Model matematika suatu fenomena adalah suatu ekspresi matematika yang diturunkan dari fenomena tersebut. Ekspresi dapat berupa persamaan, sistem persamaan atau ekspresi-ekspresi matematika yang lain seperti fungsi maupun relasi. Model matematika digunakan untuk menjelaskan karakteristik fenomena yang dimodelkannya, dapat secara kualitatif atau kuantitatif. Dalam memperoleh, membuat, mengembangkan atau menurunkan model matematika kita melibatkan asumsi-asumsi, pendekatan-pendekatan maupun pembatasan-pembatasan yang didasarkan atas eksperimen maupun observasi terhadap fenomena sebenarnya. Asumsi, pendekatan maupun pembatasan ini digunakan untuk mempelajari fenomena tersebut secara sederhana (penyederhanaan fenomena sesungguhnya), dan juga seringkali digunakan untuk mempelajari kontribusi faktor-faktor tertentu dengan tiadanya faktor yang lain pada fenomena yang dipelajari.

Pemodelan matematika merupakan salah satu tahap dari pemecahan masalah matematika. Pembahasan pemodelan matematika dimulai dari pengertian model dan kegunaannya. Kemudian tahap-tahap pembentukan model matematika dibahas satu persatu dan diberikan contoh-contohnya. Sebelum pembahasan mengenai hal-hal tersebut, berikut ini diberikan alasan mengapa pemodelan matematika perlu dan penting untuk dipelajari. Metode pembelajaran di kelas dapat ditandai dengan beberapa hal sebagai berikut:

1.     Anak didik lebih banyak menghafal pelajaran daripada berusaha mengerti dan memahaminya;

2.     Anak didik lebih tertarik pada masalah teknis yaitu menyelesaikan soal matematika yang masalahnya telah diformulasikan di dalam bentuk persamaan atau pertidaksamaan atau sistem persamaan, tanpa berusaha menggali apa makna model itu, dan bagaimana proses yang ditempuh untuk membuat modelnya. Tampak bahwa mencari solusi dari suatu model menjadi inti masalah matematika yang harus dikuasai. Para Anak kurang dibiasakan untuk mengerti dan memahami sejak dini bahwa lambang-lambang yang menjadi cirinya yang khusus atau model matematika (apakah berupa persamaan, pertidaksamaan, sistem persamaan, atau sistem pertidaksamaan) itu hanyalah sebagaian kecil dari masalah nyata yang dihadapi;

3.     Pengajaran sekarang lebih menitikberatkan pada perkembangan intelek dan kurang memperhatikan unsur-unsur sikap. Artinya bagaimanakah sikap Anak setelah mereka terlibat aktif membahas suatu materi, apakah anak menjadi lebih bersemangat belajar dan berusaha untuk menguasai masalah-masalah berikutnya, atau sebaliknya sikap anak menjadi pasif dan tidak ada kemauan untuk mempelajari agar ia mengerti. Jika Anak makin bersemangat belajar berarti nilai-nilai dasar akan berkembang dalam pribadi anak seperti percaya diri dalam menghadapi masalah yang ada;

4.     Cara pengajaran tampak menekankan pada hasil belajar, tetapi kurang memperhatikan proses belajar. Kita menyadari bahwa sesungguhnya dalam proses inilah sering muncul sejumlah ide kreatif dan cemerlang untuk menyempurnakan pengalaman belajar. Akan tetapi jika hal ini diabaikan akan berakibat kepada kesulitan pada bagian metodologi dasar yaitu membuat model matematika dari unsur masalah yang diberikan. Hubungan dari unsur-unsur masalah nyata, abstraksi dan model dari masalah nyata yang diberikan sulit dirumuskan. Berdasarkan kenyataan di atas perlu dicarijalan keluar agar persoalan tersebut sedapat mungkin lebih mudah diatasi. Pada pembahasan ini akan dibahas masalah-masalah matematika sederhana yang berkaitan dengan proses pembentukan model matematika dari suatu masalah.

Contoh model matematika adalah:

Pertumbuhan populasi bakteri suatu jenis bakteri membelah dua setiap detik. Maka jumlah bakterinya

Y = 2 ^t dengan t = waktu (detik)

Untuk mencari kapan bakteri mencapai jumlah tertentu adalah :

t =log y/log 2

Model adalah pola (contoh, acuan, ragam) dari sesuatu yang akan dibuat atau Dihasilkan. Definisi lain dari model adalah abstraksi. Dari sistem sebenarnya, dalam gambaran yang lebih sederhana serta mempunyai tingkat prosentase yang bersifat menyeluruh, atau model adalah abstraksi dari realitas dengan hanya memusatkan perhatian pada beberapa sifat dari kehidupan sebenarnya.

Jenis-jenis model dapat dibagi dalam lima kelas yang berbeda:

1.     Kelas I, pembagian menurut fungsi

a.     Model deskriptif; hanya menggambarkan situasi sebuah sistem tanpa rekomendasi dan peramalan. Contoh : peta organisasi

b.     Model prediktif; model ini menunjukkan apa yang akan terjadi, bila sesuatu terjadi.

c.     Model normatif; model yang menyediakan jawaban terbaik terhadap satu persoalan. Model ini memberi rekomendasi tindakan-tindakan yang perlu diambil. Contoh: model budget advertensi, model economics, model marketing.

2.     Kelas II, pembagian menurut struktur

a.     Model Ikonik; adalah model yang menirukan sistem aslinya dari segi fisik, seperti bentuk, pola dan fungsi, tetapi dalam suatu skala tertentu.

Contoh: model mobil atau model pesawat terbang

b.     Model Analog; suatu model yang menirukan sistem aslinya dengan hanya mengambil beberapa karakteristik utama dan menggambarkannya dengan benda atau sistem lain secara analog. Model analog biasanya lebih mudah dimengerti daripada sistem yang digambarkannya

Contoh : aliran lalu lintas di jalan dianalogkan dengan aliran air dalam sistem pipa.

c.     Model Simbolis; suatu model yang menggambarkan sistem yang ditinjau dengan simbol-simbol biasanya dengan simbol-simbol matematik. Dalam hal ini sistem diwakili oleh variabel-variabel dari karakteristik sistem yang ditinjau.

3.     Kelas III, pembagian menurut referensi waktu.

a.     Statis; model statis tidak memasukkan faktor waktu dalam perumusannya.

b.     Dinamis; mempunyai unsur waktu dalam perumusannya.

4.     Kelas IV, pembagian menurut referansi kepastian.

a.     Deterministik; dalam model ini pada setiap kumpulan nilai input, hanya ada satu output yang unik, yang merupakan solusi dari model dalam keadaan pasti.

b.     Probabilistik; model probabilistik menyangkut distribusi probabilistik dari input atau proses dan menghasilkan suatu deretan harga bagi paling tidak satu variabel output yang disertai dengan kemungkinan-kemungkinan dari harga-harga tersebut.

c.     Game; teori permainan yang mengembangkan solusi-solusi optimum dalam menghadapi situasi yang tidak pasti.

5.     Kelas V, pembagian menurut tingkat generalitas.

a.     Umum

b.     Khusus

Proses Pemodelan Matematika

Pemodelan adalah deskriptif lengkap mengenai satu sistem dari perspektif tertentu atau suatu bentuk penyederhanaan dari sebuah elemen dan komponen yang sangat komplek untuk memudahkan pemahaman dari informasi yang dibutuhkan. Pemodelan matematika merupakan proses dalam memperoleh pemahaman matematika melalui konteks dunia nyata Dalam pemodelan matematik bahwa masalah nyata yang sering dihadapi dalam kehidupan sehari-hari perlu disusun dalam suatu model matematik sehingga, mudah dicari solusinya. Proses pembentukan model matematika melalui tahap abstraksi dan idealisasi. Dalam proses ini diterapkan prinsip-prinsip matematika yang relevan sehingga menghasilkan sebuah model matematika yang  diharapkan. Beberapa hal penting dan perlu agar model yang dibuat sesuai dengan konsep masalah antara lain, masalah itu harus dipahami karakteristiknya dengan baik, disusun formulasi modelnya, model itu divalidasi secara cermat, solusi model yang diperoleh diinterpretasikan dan kemudian diuji kebenarannya. Metodologi dasar dalam proses penentuan model matematika atau sering disebut pemodelan matematika dapat dilakukan dalam beberapa tahapan, yaitu:

Tahap 1. Masalah; Adanya masalah nyata yang ingin dicari solusinya merupakan awal kegiatan penyelidikan. Masalah tersebut harus diidentifikasi secara jelas, diperiksa dengan teliti menurut kepentingannya. Bila masalahnya bersifat umum maka diupayakan menjadi masalah khusus atau operasional.

Tahap 2. Karakterisasi masalah; Masalah yang diteliti diperlukan karakterisasi masalahnya, yaitu pengertian

yang mendasar tentang masalah yang dihadapi, termasuk pemilihan variabel yang relevan dalam pembuatan model serta keterkaitanya.

Tahap 3. Formulasi model matematik; Formulasi model merupakan penterjemahan dari masalah kedalam persamaan matematik yang menghasilkan model matematik. Ini biasanya merupakan tahap (pekerjaan) yang paling penting dan sukar. Makin paham akan masalah yang dihadapi dan kokoh penguasaan matematik seseorang, akan sangat membantu memudahkan dalam mencari modelnya. Dalam pemodelan ini kita selalu berusaha untuk mencari model yang sesuai tetapi sederhana. Makin sederhana model yang diperoleh untuk tujuan yang ingin dicapai makin dianggap baik model itu. Dalam hal ini model yang digunakan ada-kalanya lebih dari satu persamaan bahkan merupakan suatu sistem, atau suatu fungsi dengan variabel-variabel dalam bentuk persamaan parameter. Hal ini tergantung anggapan yang digunakan. Tidak tertutup kemungkinan pada tahap ini juga dilakukan "coba", karena model matematik ini bukanlah merupakan hasil dari proses sekali jadi.

Tahap 4. Analisis; Analisis matematik kemudian dilakukan dengan pendugaan parameter serta deduksi sifat-sifat yang diperoleh dari model yang digunakan.

Tahap 5. Validasi; Model umumnya merupakan abstraksi masalah yang sudah disederhanakan, sehingga hasilnya mungkin berbeda dengan kenyataan yang diperoleh. Untuk itu model yang diperoleh ini perlu divalidasi, yaitu sejauh mana model itu dapat dianggap memadai dalam merepresentasikan masalah yang dihadapi. Proses

validasi ini sebenarnya sudah dimulai dalam tahap analisis, misalnya dalam hal konsistensi model terhadap kaedah-kaedah yang berlaku.

Tahap 6. Perubahan; Apabila model yang dibuat dianggap tidak memadai maka terdapat kemungkinan bahwa formulasl model yang digunakan atau karakterisasi masalah masih banyak belum layak (sesuai), sehingga perlu diadakan perubahan untuk kemudian kembali ke tahap berikutnya.

Tahap 7. Model memadai; Bila model yang dibuat sudah memadai, maka tahap berikutnya dapat dilakukan. Model tersebut dapat digunakan untuk mencari solusi masalah yang diinginkan. Model suatu masalah akan sangat terkait dengan tujuan yang diinginkan. Masih terdapat kemungkinan bahwa model yang kita anggap memadai saat ini, dengan makin bertambahnya informasi yang terkumpul, suatu waktu nantinya mungkin dianggap tidak lagi memadai. Apalagi pengamatan yang kita lakukan hanyalah merupakan sebagian informasi yang tersedia. Dalam tahap ini dilakukan interpretasi keluaran darimodel dan dikonsultasikan pada bahasa

masalah semula.

Keseluruhan tahapan di atas dapat dilihat pada Bagan berikut:

 Pemodelan matematika merupakan proses dalam memperoleh pemahaman matematika melalui konteks dunia nyata. Menurut Lovitt (1991) pemodelan matematika ditandai oleh dua ciri utama, yaitu

1.     pemodelan bermula dan berakhir dengan dunia nyata,

2.     pemodelan membentuk suatu siklus.

Pemodelan matematika adalah penyusunan suatu deskripsi dari beberapa perilaku dunia nyata (fenomena-fenomena alam) ke dalam bagian-bagian matematika yang disebut dunia matematika (mathematical world). Pemodelan matematika juga merupakan representasi dari objek, proses, atau hal lain yang diharapkan dapat diketahui polanya sehingga dapat dianalisis. (Dym and Ivey, 1980) Pemodelan matematika adalah penyusunan suatu deskripsi dari beberapa perilaku dunia nyata (fenomena-fenomena alam) ke dalam bagian-bagian matematika yang disebut dunia matematika. Ada dua tipe model matematika, yaitu model bertipe deterministik dan model bertipe empirik. Model deterministik merupakan suatu model matematika yang dibangun berlandaskan hukum-hukum atau sifat-sifat yang berlaku pada sistem. Sedangkan model empiric lebih cenderung kepada fakta yang diberikan oleh sistem atau data. (Giordano dan Weir, 2002) Pemodelan matematika merupakan bidang matematika yang berusaha untuk merepresentesi dan menjelaskan sistem-sistem fisik atau problem di dunia real dalam pernyataan matematik sehingga diperoleh pemahaman dari problem dunia real ini menjadi lebih tepat.

Model matematika yang dihasilkan, baik dalam bentuk persamaan, pertidaksamaan, sistem persamaan atau lainnya terdiri atas sekumpulan lambang yang disebut variabel atau besaran yang kemudian didalamnya digunakan operasi matematika seperti tambah, kali, kurang, atau bagi. Dengan prinsip-prinsip matematika tersebut dapat dilihat apakah model yang dihasilkan telah sesuai dengan rumusan sebagaimana formulasi masalah nyata yang dihadapi. Hubungan antara komponen-komponen dalam suatu masalah yang dirumuskan dalam suatu persamaan matematik yang memuat komponen-komponen itu sebagai variabelnya, dinamakan model matematik. Dan proses untuk memperoleh model dari suatu masalah dikatakan pemodelan matematika.

Terdapat beberapa jenis model matematika antara lain :

1.     Model empiris; pada model empiris data yang berhubungan dengan problem menentukan peran yang penting. Dalam pendekatan ini gagasan yang utama adalah mengkronstruksi formula (persamaan) matematika yang dapat menghasilkan grafik yang terbaik untuk mencocoan data.

2.     Model simulasi; Dalam pendekatan ini program komputer dituliskan didasarkan pada aturan-aturan yang dipercaya untuk membentuk suatu proses

3.     Model stokastik dan Deterministik; Model Stokastik adalah model matematika dimana gejala-gejala dapat diukur dengan derajat kepastian yang tidak stabil. Pada Model Stokastik disebut juga model probabilistik peluang dari masing-masing kejadian benar-benar di hitung, menyusun sebuah model stokastik cenderung lebih sulit dari model deterministik. Kaidah-kaidah peluang adalah alat matematika yang cukup vital dalam menyusun model stokastik. Contoh model stokastik adalah teori antrian dan teori permainan, dimana ini merupakan pengembangan dari riset operasi modern.

Model dan Kegunaannya

Dalam kehidupan sehari-hari, kata model sering digunakan, dan mengandung arti sebagai contoh, miniatur, peta, imejsebagai representasi dari suatu masalah. Misalnya, model pakaian, model rumah. Secara umum istilah tersebut di atas menggambarkan adanya padanan atau hubungan antara unsur-unsur dari rumah dengan modelnya. Sebagai contoh, perbandingan antara panjang dan lebar bangunan rumah dengan modelnya. Tetapi tidaklah berarti bahwa model rumah dan rumah itu sendiri sama ukuranya dalam setiap hal. Secara singkat dapat dikatakan bahwa apabila ada suatu benda A (dapat berupa masalah, fenomena) dan modelnya B, maka terdapat kumpulan unsur-unsur dam B yang mempunyai padanan dengan A. Demikian pula terdapat suatu hubungan yang berlaku antara unsur-unsur di B yang sesuai dengan unsur-unsur sebagai padanannya di A. Dengan analogi pemikiran seperti itu, dalam matematika pun selalu terkait pada masalah yang berhubungan dengan besaran atau variabel. Suatu fenomena atau sebuah unsur tertentu dapat direpresentasikan dengan suatu variabel. Suatu

masalah yang timbul akan lebih mudah dan menjadi tampak sederhana, apabila masalah itu dinyatakan secara matematik.

Contoh pemodelan matematika adalah:

Misalnya, mutu lulusan sekolah dasar (M), tergantung atas beberapa faktor, seperti kualitas guru (x₁), kualitas masukan (x₂), relevansi kurikulum (x₃), dan sarana penunjang pembelajaran (x₄). Jika disusun rumusan unsur-unsur ini, dapat dinyatakan bahwa mutu lulusan adalah fungsi dari faktor-faktor x₁, x₂, x₃, dan x₄. Dalam bentuk model matematik hubungan ini dapat ditulis dengan M = F(x₁, x₂, x₃, x₄) atau secara singkat ditulis M = f(x), dengan pemahaman bahwa variabel x mewakili variabel x₁, x₂, x₃ dan x₄. Bentuk penulisan terakhir ini menunjukkan adanya simplikasi (penyederhanaan) cara penulisan hubungan antara variabel yang satu dengan variabel lainnya. Perihal mutu lulusan yang dipengaruhi oleh mutu guru, mutu masukan, relevansi kurikulum dan sarana penunjang lainnya merupakan kondisi obyektif suatu fakta yang secara realitas terjadi di sektor pendidikan. Kondisi nyata demikian diabstraksikan kemudian ketidaksempurnaan yang terdapat pada masing-masing unsur dieliminir dan dipandang telah sesuai dengan kondisi sesungguhnya. Proses ini disebut proses abstraksi dan idealisasi. Dalam proses ini diterapkan prinsip-prinsip matematika yang relevan sehingga menghasilkan sebuah model matematika yang diharapkan.

Model matematika yang dihasilkan, baik dalam bentuk persamaan, pertidaksamaan, sistem persamaan atau lainnya terdiri atas sekumpulan lambang yang disebut variabel atau besaran yangkemudian di dalamnya digunakan operasi matematika seperti tambah, kali, kurang, atau bagi. Dengan prinsip-prinsip matematika tersebut dapat dilihat apakah model yang dihasilkan telah sesuai dengan rumusan sebagaimana formulasi masalah nyata yang dihadapi. Hubungan antara komponen-komponen dalam suatu masalah yang dirumuskan dalam suatu persamaan matematik yang memuat komponen-komponen itu sebagai variabelnya, dinamakan model matematik. Dan proses untuk memperoleh model dari suatu masalah dikatakan pemodelan matematika. Kegunaan yang dapat diperoleh dari model matematika ini antara lain:

1.     Menambah kecepatan, kejelasan, dan kekuatan-kekuatan gagasan dalam jangka waktu yang relatif singkat,

2.     Deskripsi masalah menjadi pusat perhatian,

3.     Mendapatkan pengertian atau kejelasan mekanisme dalam masalah,

4.     Dapat digunakan untuk memprediksi kejadian yang akan muncul dari suatu fenomena atau perluasannya,

5.     Sebagai dasar perencanaan dan kontrol dalam pembuatan kebijakan.

Gagasan yang dinyatakan dalam bentuk fungsi matematika merupakan salah satu generalisasi yang besar. Pada umumnya, fungsi matematika itu menyatakan kepada kita, bagaimana obyek-obyek dalam suatu himpunan masalah berhubungan satu dengan yang lain, Misalnya, bagaimana hubungan panjang lintasan (S), kecepatan (v), dan waktu (t) dari suatu benda yang bergerak. Formulasi dari hal tersebut dalam model matematika adalah 

S = f (v,t) = vt

Contoh lain, bagaimana hubungan antara luas (L) bangun segitiga dan panjang alas (a) dan tinggi (t) segitiga. Dalam hal ini, kita pahami bahwa luas bangun segitiga tergantung atas panjang alas dan tingginya. Formulasi yang menunjukkan hubungan tersebut dinyatakan oleh

L = ½ at

Klasifikasi Pembentukan Model

Suatu model seringkali dikelompok-kelompokkan antara lain berdasar upaya memperolehnya, keterkaitan pada waktu atau, sifat keluarannya. Model yang disamarkan atas upaya memperolehnya misalnya adalah model teoritik, meknistik, dan empiris.

1.     Model teoritik digunakan bagi model yang diperoleh dengan menggunakan teori-teori yang berlaku. Model mekanistik digunakan bila model tersebut diperoleh berdasar maknisme pembangkit fenomena.

2.     Model empirik digunakan bagi model yang diperoleh hanya dari pengamatan tanpa didasarkan pada teori atau pengetahuan yang membangkitkanfenomena tersebut.

3.     Model mekanistik dapat digunakan untuk lebih mengerti tentang proses pembangkit fenomena, biasanya lebih sedikit parameternya, serta luas kawasan berlakunya.

Bila mekanisme fenomena tersebut sukar dipahami, maka model empirik akan sangat berguna. Model yang didasarkan akan keterkaitan pada waktu adalah model statik dan dinamik. Model statik adalah model yang tidak terkait pada waktu sedangkan model dinamik tergantung pada waktu. Bila perubahan dalam model dinamik terjadi atau diamati secara kontinu dalam waktu, maka model tersebut dikatakan sebagai model diskrit. Bila keluaran suatu model dapat ditentukan secara pasti, yang tentunya berpadanan dengan hasil dari fenomenanya, maka model disebut sebagai model deterministik. Jika tidak, berarti ada ketidakpastian dari keluarannya, yang biasanya disebut sebagai variabel acak, maka model tersebut dikatakan sebagai model stokastik. Jadi, dalam model stokastik keluarannya tidak sepenuhnya dapat dispesifikasikan oleh bentuk model dan parameternya, tapi mengandung variabel lain yang tak dapat ditentukan secara pasti. Umumnya tak ada kepastian sesuainya keluaran suatu model, tetapi bila ketidakpastian itu dapat diabaikan maka model deterministik tersebut cukup memadai untuk digunakan.

PEMBENTUKAN MODEL MATEMATIK SEDERHANA

Pembentukan model matematik dari suatu masalah dengan langkah-langkah yang telah disebutkan di atas terlalu luas untuk diterapkan. Dalam masalah yang sifatnya sederhana dapat dipilih strategi pemecahan di bawah ini.

Langkah 1. Baca masalah dengan cermat kemudian tentukan apa yang diketahui, dan apa yang belum diketahui atau dicari. Tulis dengan lengkap informasi ini.

Langkah 2. Gunakan variabel untuk menyatakan apa yang dicari atau ditanyakan.

Langkah 3. Konstruksi diagram atau bagan untuk memudahkan atau menentukan hubungan yang ada antara unsur-unsur dan variabel yang diketahui.

Langkah 4. Nyatakan model matematik yang dicari dalam bentuk persamaan atau pertidaksamaan atau sistem persamaan.

Teladan 1  :    Sebuah bidang berbentuk persegi panjang dengan selisih panjang dan lebar sama dengan 4 dm. Jika luas bidang 96 dm², formulasikanlah suatu fungsi untuk menyatakan luas bidang tersebut.

Penyelesaian:

Langkah 1  :    Diketahui:     Bidang berbentuk persegi panjang,

                                        Selisih panjang dan lebar sama dengan 4 dm,

                                        Luas bidang 96 dm²

Ditanyakan:   Formulasi matematik yang menyatakan luas bidang.

Langkah 2  :    Misalkan panjang bidang adalah x, sehingga lebar bidang tersebut adalah x– 4. Sedangkan luas bidang adalah 96 dm², dan luas bidang ini adalah panjang kali lebar.

Langkah 3  :    Diagramnya

Panjang	x
Lebar	x - 4
Luas L(x)	Panjang kali lebar

Langkah 4  :    Formulasi fungsi untuk luas bidang adalah L(x) = x(x - 4)

                     karena luas bidang sama dengan 96 dm²

                     maka diperoleh x(x – 4) = 96

                     Jadi untuk masalah di atas diperoleh model matematika x(x - 4) = 96

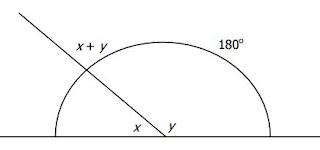
Teladan 2  :    Jumlah dua buah sudut 180 derajat. Besar salah satu sudut 1½ kali besar sudut lainnya. Formulasikan suatu sistem persamaan yang menyatakan hubungan antara unsur-unsur masalah yang diketahui guna mencari besarnya masing-masing sudut.

Penyelesaian:

Langkah 1  :    Diketahui:     Jumlah dua sudut adalah 180 derajat

                                        Besar salah satu sudut sama dengan 1½ kali besar sudut lainnya

                     Ditanyakan:   Formulasi sistem persamaan yang menyatakan hubungan antara unsur-unsur masalah

Langkah 2  :    Misalkan ukuran sudut terkecil adalah x, dan sudut terbesar adalah y

                     Jumlah kedua sudut x + y adalah 180 derajat.

`Langah 3    :    Gambar sudutnya

Langkah 4:      Karena jumlah sudut x dan y adalah 180^o, maka persamaannya adalah x + y = 180.

                     Sudut terbesar  y = 1½x

                     Jadi model matematika dari masalah di atas diperoleh sistem persamaan linear dengan dua variabel yaitu

Teladan 3  :    Sebuah kebun berbentuk persegi panjang ingin dipagari dengan 100 meter pagar kawat. Jika salah satu sisi kebun adalah tembok yang tidak perlu dipagari, rumuskanlah suatu fungsi yang menyatakan luas kebun untuk dipagari kawat berdasarkan informasi yang ada pada masalah itu.

Penyelesaian:

Langkah 1  :    Diketahui:     Sebuah kebun berbentuk persegi panjang.

                                         Kawat yang tersedia 100 meter.

                                        Salah satu sisi panjang tak perlu diberi pagar.

                     Ditanyakan:   Model matematik yang menyatakan luas kebun.

Langkah 2  :    Misalkan panjang dan lebar kebun masing-masing adalah x dan y meter.

                     Bagian kebun yang ingin dipagari adalah 2x + y = 2 meter.

                     Karena panjang pagar kawat yang tersedia adalah 100 meter, diperoleh hubungan 2x + y = 100

Langah 3    :    Gambar kebun sebagai berikut

 
Langkah 4  :    Dari persamaan  2x + y = 100 diperoleh y = 100 – 2x.

                        Misalkan luas kebun dinyatakan dengan  L(x), maka model matematika yang dicari adalah

L(x) = xy = x(100 – 2x) = 100x – 2x²

Pendalaman:

1.     Selisih dua bilangan bulat positif adalah 42, dan jumlahnya 86. Tentukanlah model matematika untuk masalah tersebut.

2.     Sebidang tanah berbentuk jajar genjang, panjang alasnya 7 meter lebih panjang dari tingginya. Jika luas tanah itu adalah 30 m², carilah persamaan yang menyatakan luas tanah tersebut.

3.     Dalam suatu lomba Matematika, Fisika dan Bahasa Inggris tercatat jumlah peserta sebanyak 41 siswa. Peserta lomba matematika tercatat 7 siswa lebih banyak dari penggemar Fisika, sedangkan peserta lomba Fisika 2 siswa lebih banyak dari peserta lomba Bahasa Inggris. Tuliskan model matematika yang menyatakan jumlah peserta lomba tersebut.

4.     Sebuah bidang berbentuk persegi panjang, panjangnya 15 meter lebih besar dari lebarnya. Jika keliling 70 meter, tuliskan formulasi matematika yang menyatakan keliling bidang itu.

5.     Pada waktu Ani lahir umur ayahnya adalah 29 tahun. Jika jumlah umur ayah dan Ani adalah 61 tahun, tulislah formulasi matematika yang menyatakan jumlah umur keduanya.